Clustering of wind resource data for the South African renewable energy development zones

Abstract

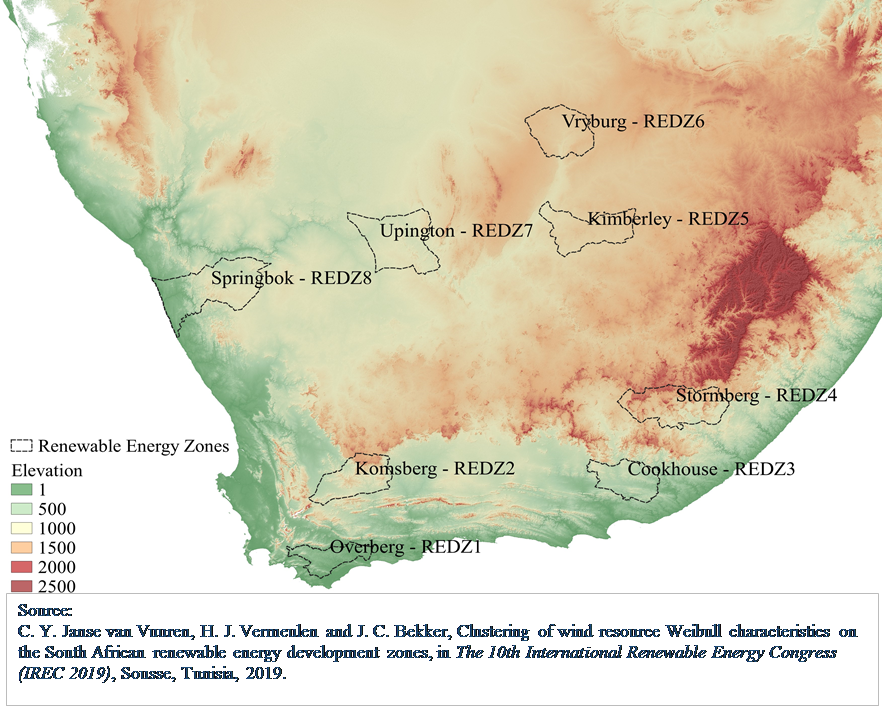
This study investigates the use of clustering methodologies as a means of reducing spatio-temporal wind speed data into statistically representative classes of temporal profiles for further processing and interpretation. The clustering methodologies are applied to the high-resolution spatio-temporal, meso-scale renewable energy resource dataset produced for Southern Africa by the Council of Scientific and Industrial Research. This large dataset incorporates thousands of coordinates and represents a challenge from a computational perspective. This dataset can be reduced by applying clustering techniques to classify the temporal wind speed profiles into categories with similar statistical properties. Various clustering algorithms are considered, with the view to compare the performances of these algorithms for large wind resource datasets, namely k-means, partitioning around medoids, the clustering large applications algorithm, agglomerative clustering, the divisive analysis algorithm and fuzzy c-means clustering. Two distance measures are considered, namely the Euclidean distance and Pearson correlation distance. The validation metrics evaluated in the investigation includes the silhouette coefficient, the Calinski-Harabasz index and the Dunn index. Case study results are presented for the Komsberg Renewable Energy Development Zone, located in Western Cape, South Africa. This zone is selected based on the high mean wind speed and large standard deviation exhibited by the temporal wind speed profiles associated with the zone. The effects of seasonal variation in the temporal wind speed profiles are considered by partitioning the input dataset in accordance with the low and high demand seasons defined by the Megaflex Time of Use tariff. The clustered wind resource maps produced by the proposed methodology represent a valuable input dataset for further studies such as siting and the optimal geographical allocation of wind generation capacity to reduce the variability and ramping effects that are inherent to wind energy.